Simpson's Paradox

Simpson’s Paradox, otherwise known as the Yule-Simpson Effect, is a reversal paradox where the correlation found in each of several groups either disappears or even reverses when the groups are combined. It’s relevant in the context of many non-experimental studies, including A/B tests.

Examples of the Paradox

One classic example of Simpson’s Paradox is from a 1975 study of sex bias in graduate admissions at the University of California, Berkeley. When considering the overall figures, there was a significant difference between the percentage of male versus female applicants admitted (44% out of 8,442 men were admitted, vs. 35% out of 4,321 women). However, when considering individual departments, the data showed a statistically significant bias in favor of women (6 out of the 85 departments were significantly biased against men, while only 4 were significantly biased against women). How can this be? It seems counterintuitive that this result is even possible. Perhaps a graph will help:

: Image source: Wikipedia

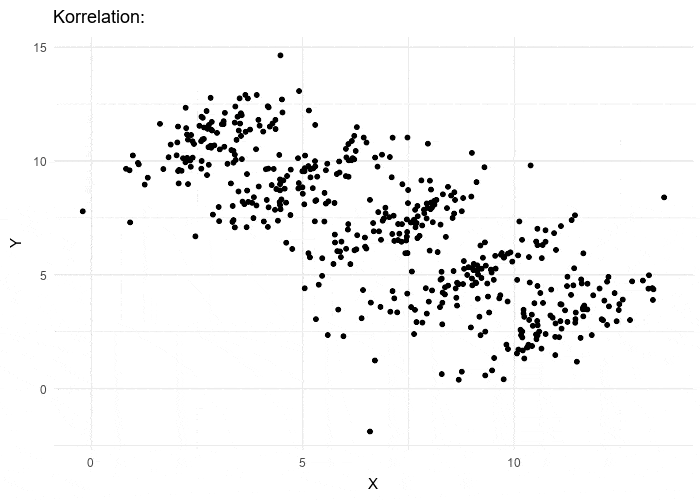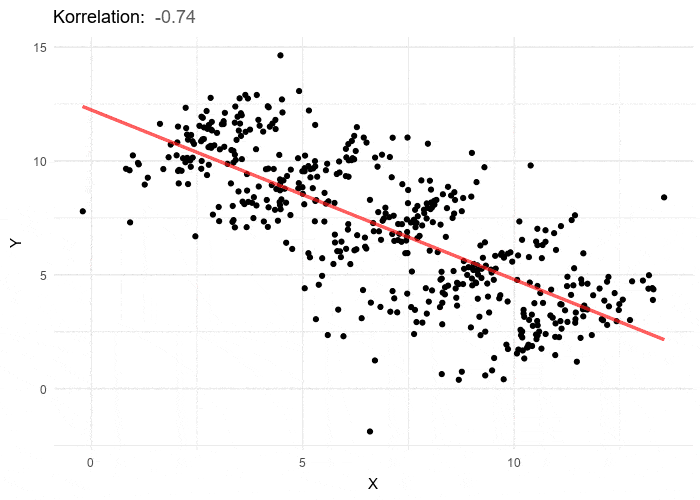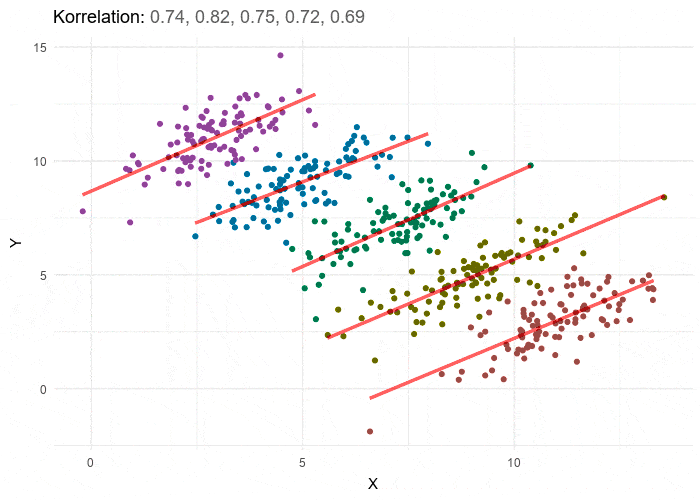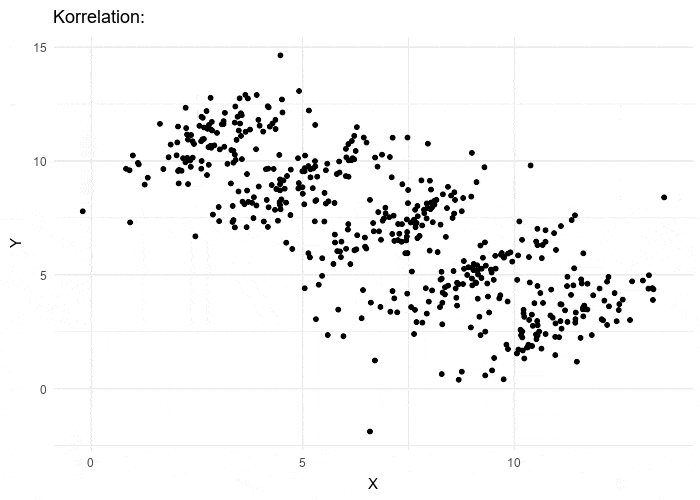
Each group’s individual correlation is positive, but the overall correlation is negative because if we took each cluster’s center as a data point, the trend of those data points would be negative. This points to the existence of a confounding variable: in the admissions study, this is that women tend to apply to more competitive departments (such as social sciences), while men tend to apply to less competitive ones (such as natural sciences). Let’s look at another real-life example.

Kidney Stone Surgeries

In a medical study, two types of kidney stone treatments were compared: Treatment A (including all open surgical procedures) and Treatment B (a specific, less invasive surgery involving a small puncture). The result was that Treatment A was more effective for small stones (93% success rate vs. 87% for Treatment B) and large stones (73% vs 69%), but Treatment B was more effective when considering both groups together (83% vs 78%). In this situation, the confounding variable is the severity of the case: doctors are more likely to prescribe the overall less effective but also less invasive Treatment B for less severe cases, whereas more severe cases are commonly prescribed Treatment A. Since more severe cases have a lower base recovery rate, this pulls down the perceived effectiveness of the treatment disproportionately used for them.

A/B Testing

In a hypothetical example, say that a development team is running two variants of a feature for their web application. The metric they’re focused on is conversion rate, and they’re running the test across two different browsers (Firefox and Chrome). They assign 80 of 100 Firefox users to Variant A (and the remainder to Variant B), and assign 20 of 100 Chrome users to Variant A (and the remainder to Variant B). The conversion rate of Variant B is found to be superior in each browsers individually (100% in Firefox compared to Variant A’s 87.5%, and 62.5% in Chrome compared to Variant A’s 50%). However, when considering both at once, Variant A is the winner (80% overall). The confounding variable here is sample size in each browser. The number of users assigned to each variant is significantly different (80 vs 20). As such, the total conversion rate numbers for Variant A is dominated by Firefox, which has a higher conversion rate, whereas the numbers for Variant B are dominated by Chrome, which has a lower conversion rate. If the numbers were equal, we would find that Variant B is the overall winner.

Considering Simpson’s Paradox

When considering any instance of Simpson’s Paradox, it’s critical to look for an un-controlled-for third variable (such as department competitiveness, case severity, or sample size), which explains the paradox. Further, since the mathematics allows perfectly well for a difference between aggregate associations and associations in individual groups, the seeming “paradox” of Simpson’s paradox arises from inappropriate use of causal inference in non-experimental studies – that is, mistaking correlation for causation. When considering whether an admissions program is biased, we don’t care only about the correlation between the sex of a student and the state of their admission, we care about whether a university department may be biased against certain students. Determining which of the two relationships – that of the department or that of the whole university – is spurious is dependent, not on statistics, but on other information about the problem. No generalizable conclusion can be drawn about which relationship is relevant, in instances of Simpson’s Paradox. In A/B testing in particular, sample size is the most common confounding variable. This makes it easier to detect Simpson’s Paradox and correct it in your feature experimentation. So long as users are evenly distributed between variants, browsers, and any other potentially-relevant categories, Simpson’s Paradox is unlikely to show up and confuse your results.

Get Split Certified

Split Arcade includes product explainer videos, clickable product tutorials, manipulatable code examples, and interactive challenges.

Deliver Features That Matter, Faster. And Exhale.

Split is a feature management platform that attributes insightful data to everything you release. Whether your team is looking to test in production, perform gradual rollouts, or experiment with new features–Split ensures your efforts are safe, visible, and highly impactful. What a Release. Get going with a free account, schedule a demo to learn more, or contact us for more information.